Vuosien mittaaminen on tuottanut paljon informaatiota metsän toiminnasta ja eri prosesseista kuten yhteyttämisestä, haihdunnasta ja hengityksestä. Tiedämme suurin piirtein, miten puu toimii eri vuodenaikoina vaihtuvissa valo-, maankosteus- ja lämpötilaoloissa. Tämä tieto voidaan ilmaista matemaattisilla malleilla, joilla voidaan myös ennustaa puun tulevaa käyttäytymistä. Matemaattinen mallintaminen on tutkimusmaailmassa tyypillinen tapa kuvata ilmiöitä eksaktisti ja tiiviissä muodossa. Malleja tarkastellessa on kuitenkin aina muistettava, ettei malli kerro todellisuudesta muuta kuin mallin muuttujien verran.
Sivujen Hiilipuu-animaatio esittää yhteytysnopeutta, joka on laskettu melko suoraviivaisilla ja yksinkertaistetuilla matemaattisilla malleilla käyttäen Hyytiälässä mitattua säätä ja maan olosuhteita. Malli sisältää yleisimmät ympäristövasteet, kun taas esimerkiksi kasvin sisäisen tilan muutos on suurimmaksi osaksi jätetty pois. Tämä tarkoittaa sitä, että tässä esitetyt vasteet eivät välttämättä ole samanlaisia ympäri vuoden vaan ne saattavat muuttua ajassa.
Yhteytysmalli on monikertaistava yhtälö pääasiallisista vaikuttavista ja rajoittavista tekijöistä:
P = f(LAI) • f(PAR) • Min{f(VPD), f(REW)} • f(T) • f(Tmin) • f(S) • f(CO2)
P kuvaa yhteyttämistä, tai pikemminkin hiilivuota, jonka yhteyttäminen saa aikaan, f() tarkoittaa yhtälöä ja edustaa jokaisen tekijän vaikutusta yhteytykseen.
Näin muotoiltuna kunkin hetken suurin mahdollinen yhteyttämisnopeus määräytyy lehtien pinta-alan (LAI), valon intensiteetin (PAR) ja hiilidioksidin (CO2) mukaan. Ympäristö ei kuitenkaan aina ole optimaalinen, ja silloin muut tekijät kuten ilman kosteus (VPD), vuorokauden minimilämpötila (Tmin), lämpötila (T), lämpötilahistoria (S) tai maankosteus (REW) säätävät ja rajoittavat yhteyttämisnopeutta.
Alla on esitetty kunkin tekijän vaikutus:
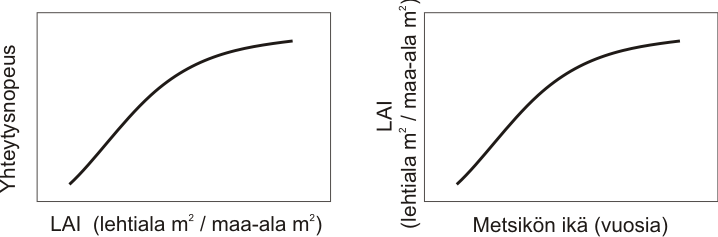
LAI (”Leaf Area Index”) tarkoittaa lehtialaindeksiä, mikä kuvaa lehtien määrää latvuksessa. Periaatteessa lehtien määrän kasvaessa myös yhteyttämisnopeus kasvaa. Lehdet kuitenkin varjostavat toisiaan joten puu kohdentaa voimavaroja lehtiin eri tavoin latvuksen eri osissa. Näin ollen LAIn kasvaessa latvuksen yhteyttämisnopeus kasvaa hidastuen.
LAI:n ja yhteytyksen suhde voidaan ilmasta matemaattisesti:
f(LAI)= 1 / K * (1 –e–K * LAI).
Mittausasemallamme Hyytiälässä LAI = 8 m2/m2ja K = 0.18.
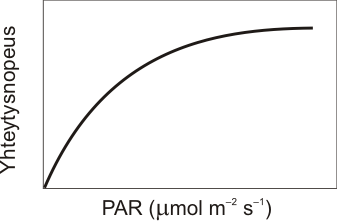
PAR (”Photosynthetically Active Radiation”) tarkoittaa valon intensiteettiä. Valon vaikutus yhteyttämisnopeuteen on kyllästyvä ts. pienillä valon intensiteeteillä valon lisääntyminen vaikuttaa yhteyttämisnopeuteen voimakkaasti, mutta kirkkaassa valossa yhteyttämiskoneisto toimii jo täydellä teholla eikä kasvi siis voi enää hyötyä valon lisääntymisestä eli nopeuttaa yhteyttämistä.
PAR-säteilyn ja yhteytyksen välisen suhteen voi ilmaista matemaattisesti yhtälöllä:
f(PAR) = Pmax * PAR / (PAR + B).
Mittausasemallamme Hyytiälässä Pmax= 9 µmol m–2 s–1 ja B = 600 µmol m–2 s–1.
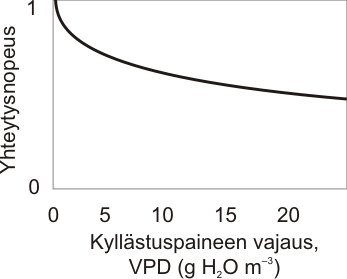
VPD (”Vapour Pressure Deficit”) tarkoittaa ilman kyllästyspaineen vajausta. Se on ekologiselle tutkimukselle tyypillinen suure kuvaamaan ilmankosteutta. Mitä suurempi vajaus, sitä kuivempaa ilma on. Haihdunta eli veden kulkeutuminen kasvista ilmaan lisääntyy, kun ilma kuivuu. Kasvi stressaantuisi ja saattaisi jopa kuivua ilman haihdunnan kontrolloimista. Liian vedenhävikin minimoimiseksi ilmaraot eli lehden pinnalla olevat huokoset sulkeutuvat sen verran, että kasvi pystyy selviytymään, sillä vesi haihtuu juuri näiden ilmarakojen kautta. Toisaalta ilmarakojen kautta hiilidioksidi kulkeutuu ilmasta lehtiin, joten ilmarakojen sulkeutuminen hidastaa haihdunnan lisäksi myös yhteyttämistä.
VPD:n yhteyttämistä rajoittavan suhteen voi ilmaista matemaattisesti näin:
f(VPD)= e–H*VPD.
Mittausasemallamme Hyytiälässä H = 0.02.
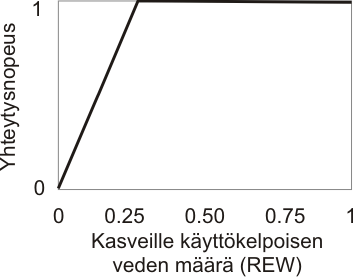
REW (”Relative Extractable Water”) tarkoittaa kasveille vapaan veden määrää maassa. Maan kuivuminen aiheuttaa lehdissä samanlaisen reaktion kuin suuri VPD eli kuiva ilma: ilmaraot sulkeutuvat ja hiilidioksidin virtaus lehtiin hidastuu, mistä seuraa myös yhteyttämisen hidastuminen.
REW:n yhteyttämistä rajoittavan suhteen voi ilmaista matemaattisesti näin:
jos REW ≥ REWCRIT, f(REW) = 1,
jos REW < REWCRIT, f(REW) = Max { 0 , REW / REWCRIT }.
Mittausasemallamme Hyytiälässä REWCRIT = 0.45.
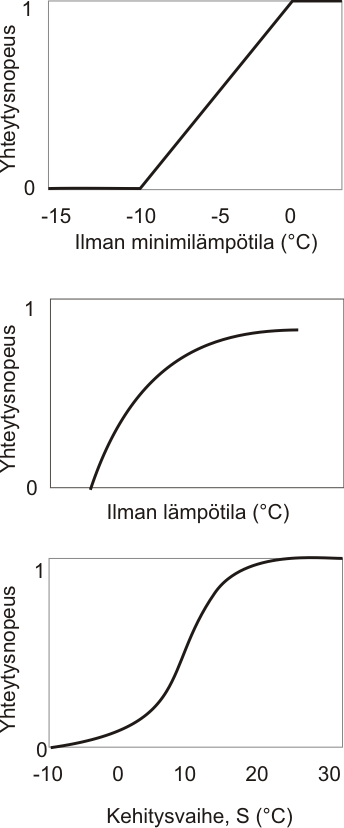
T eli lämpötila vaikuttaa yhteytysnopeuteen kolmella eri tavalla ottaen huomioon viimeisen 24 tunnin minimilämpötilan (Tmin), hetkellisen lämpötilan (T) ja lämpötilahistorian (S). Jos viimeisen 24 tunnin minimilämpötila on alle nollan, laskee yhteytysnopeus ja jos lämpötila on ollut alle kymmenen pakkasastetta, yhteytystä ei tapahdu ollenkaan. Matemaattisesti se voidaan ilmasta näin:
f(Tmin) = Max { 0 , Min { 1, (T0min – Tmin ) / T0min } }.
Mittausasemallamme Hyytiälässä T0min = –10 °C.
Kasvin valmius yhteyttää on erilainen eri vuodenaikoina: maksimi kesällä, minimi talvella jne. Tätä prosessia säätelee lähinnä ilman lämpötila. S (”Stage of acclimation”) kuvaa yhteyttämisnopeuden kausiluonteisuutta eli kasvin sopeutumista muuttuvaan lämpötilaan. S edustaa kasvin kykyä seurata ja tahdistaa biologinen aktiivisuus vuodenajan tarjoamien mahdollisuuksien mukaiseksi kuitenkin riskejä kuten hallatuhoja minimoiden. Päivittäinen S riippuu lämpötiloista, jonka kasvi on kokenut edellisten päivien kuluessa. S seuraa ilman lämpötilaa aikavakiolla τ, joka yleensä on 150 h. Tämä voidaan ilmaista aikaderivaattana:
dS/dt = ( T(t) – S(t) ) / τ .
S:n vaikutus yhteytykseen voidaan ilmaista matemaattisesti näin:
f(S) = 1 / (1 + ec*(S–TS) ).
Mittausasemallamme Hyytiälässä c = –0.25 ja TS = 5.5°C .
Hetkellisen ilman lämpötilan vaikutus voidaan ilmaista näin:
f(T)=1–ecT*(T–T0).
Mittausasemallamme Hyytiälässä
T0 = –5 °C ja cT = Min {-0.1, 0.5 * ( f(S)–1) }
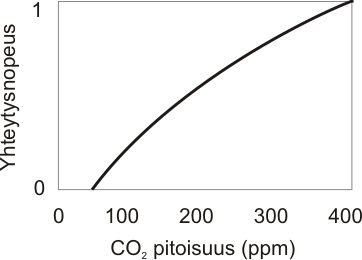
CO2. Mitä enemmän hiilidioksidia on ilmassa, sitä enemmän on yleensä yhteytystäkin, kunhan muut olosuhteet ovat kohdallaan. Hiilidioksidin yhteytystä rajoittavaa suhdetta voi kuvata matemaattisesti näin:
f(CO2)=(CO2 – γ) / (CO2 + γ + KCO2) * (CO2ref + γ + KCO2 ) / (CO2ref – γ).
Mittausasemallamme Hyytiälässä CO2ref=400 ppm, γ=50 ppm ja KCO2=500 ppm.
Samantyyppisen mallin yksityiskohtainen kuvaus:
Mäkelä, A., Pulkkinen, M., Kolari, P., Lagergren, F., Berbigier, P., Lindroth, A., Loustau, D., Nikinmaa, E., Vesala, T., and Hari, P. 2008. Developing an empirical model of stand GPP with the LUE approach: analysis of eddy covariance data at five contrasting conifer sites in Europe. Global Change Biology, 14, 92-108.